Learning about different types of angles is important because these angles form the base of geometry. When two lines intersect, they form an angle at the point of intersection. The various types of angles based on their measurements are acute angle, right angle, obtuse angle, reflex angle, etc. The rays that are forming an angle are known as the sides of the angle. An angle is formed by the intersection of two straight or curved lines. We can measure these angles in degrees. The whole turn of an angle is 360 degrees. The angle is derived from the Latin word Angulus.
What is the angle?
In plane geometry, a figure that is formed by joining two rays is called an angle. These two rays are the sides of the angle. These two rays share a common endpoint. This is the vertex of the angle. By using angles, we can describe the space between two lines. These two lines begin at the same point. One can measure angles in degrees. We use a protractor to measure angles. One can measure angles from 0° to 360° in a circle. We use angles throughout the geometry. If we want to learn geometry, we should know how to measure and describe angles.
Parts of an angle
There are two main parts of an angle. As we know that two lines join together to form an angle. These two lines are known as the arms of an angle. These two lines meet at a common endpoint. This is the vertex of an angle.

Types of angles
There are various types of angles. These various types of angles are given below;
1. Acute Angle
2. Obtuse Angle
3. Right Angle
4. Straight Angle
5. Reflex Angle
6. Full Angle
7. Zero Angle
1. Acute Angle
An acute angle is a small angle. An acute angle has a measurement of fewer than 90 degrees. In other words, an angle whose measurement is between 0 to 90 degrees is known as an acute angle.

2. Obtuse Angle
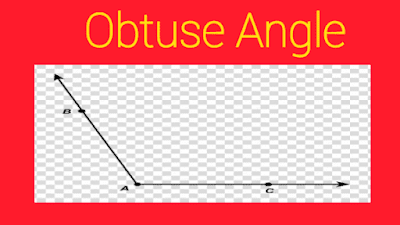
An obtuse angle is a larger angle. An angle whose measurement is greater than 90 degrees is known as an obtuse angle. In other words, an angle whose measurement is in between 90 to 180 degrees is known as an obtuse angle.
3. Right Angle
An angle that has an exact measurement of 90° is a right angle. When we place a ray at the endpoint of a line, this ray forms adjacent angles. If these adjacent angles are equal, these are right angles. When two intersecting lines are perpendicular to each other, these two lines form right angles. To represent the right angle, we use a symbol ∟. The corners of a box form right angles.

4. Straight Angle
An angle that has an exact measurement of 180° is straight. It is in the form of a straight line. We appoint the legs of the straight angle in the opposite direction.

5. Reflex Angle
A reflex angle is also a large angle. The measurement of a reflex angle is more than 180° but less than 360°. It is the most confusing angle because we have to draw it at the outer side of the line. Most of the children make mistakes while measuring reflex angles. The children can measure reflex angles in two ways. First, they can measure the reflex angle by drawing the circle. Secondly, they can measure the inner angle. After measuring the inner angle, they can subtract it from 360°. It will give a reflex angle.

6. Full Angle
Other names of the full angle are complete angle or round angle. A full angle has an exact measurement of 360°. It is the central angle of an entire circle. To form a full angle, we have to add two straight angles or four right angles.

7. Zero Angle
A zero angle has a measurement of 0°. The initial and the final arms of the zero angle are at the same position. In other words, the legs of the zero angles are in the same direction. Along with reading about types of angles with pictures, you may also like to read about types of triangles with pictures.

Types of angles based on pairs
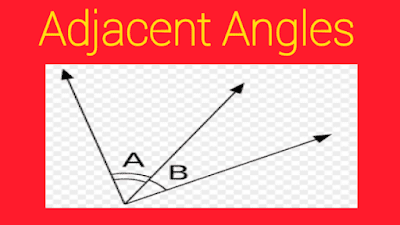
1. Adjacent Angles
If two angles have a common side and a common vertex, they are adjacent angles. The adjacent angles don’t overlap.
2. Complementary Angles
If the sum of two angles is 90°, these angles are complementary. For example, if we add 40° and 50°, their sum is 90°. These are complementary angles. The sum of 10° and 80° is also 90°. Therefore, these are also complementary angles.

3. Supplementary Angles
If the sum of two angles is 180°, these angles are supplementary. When we join supplementary angles, we get a straight angle. 150° and 30° are supplementary angles because their sum is 180°.

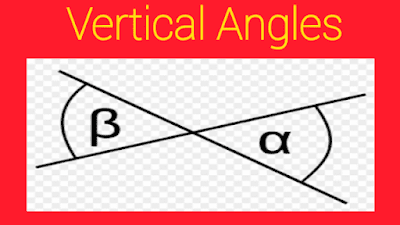
4. Vertical Angles
Two lines after crossing form four angles. The angles opposite to each other that are sharing the same vertex are vertical. We can also call them vertically opposite angles. The vertically opposite angles are equal. By using the concept of vertically opposite angles, we can find out missing angles. Therefore, we can say that vertically opposite angles are congruent. Vertical angles consist of a pair of non-adjacent angles.
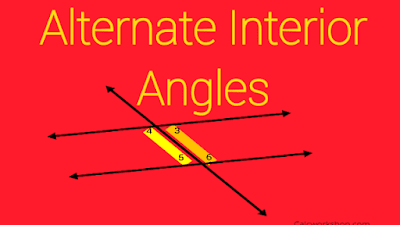
5. Alternate Interior Angles
When a transversal crosses two parallel lines, it forms eight angles. In these angles, four angles are formed outside of these parallel lines and four angles are formed inside of these parallel lines. A pair of angles inside the parallel lines that are present on opposite sides of the transversal are known as alternate interior angles. If we want to remember these angles easily, we can understand the concept that these angles are present on the interior of the crossed lines. The alternate interior angles are equal.
6. Alternate Exterior Angles
As we have discussed in the previous definition that when a transversal crosses two parallel lines, it forms four outside angles. A pair of angles outside the parallel lines that are present on the opposite sides of the transversal are known as alternate exterior angles. To remember these angles, we should understand that these angles are present on the exterior of the crossed lines. The alternate exterior angles are equal.

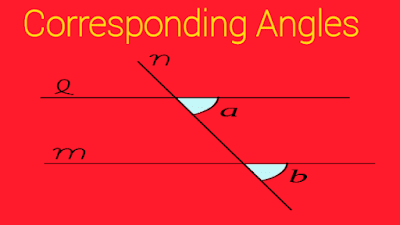
7. Corresponding Angles
When a transversal crosses two parallel lines, it forms different angles. The angles that are present at the matching corners are known as corresponding angles. The corresponding angles are equal.
Positive and Negative Angles
A positive angle goes counterclockwise. It means that it goes in the opposite direction as the clock goes. A negative angle goes clockwise. It means that it goes in the same direction as the clock goes.
Applications of Angles
We are using the concepts of different types of angles in our daily life. For example, if we want to draw hands on a clock, we have to make use of angles. The two intersecting roads also make angles. The blades of a fan are also making angles. We are also using angles for the navigation of the planes and ships. We have to make use of angles to draw various shapes like triangles, rectangles, and squares.
Properties of Angles
There are some properties of these angles. By learning these properties, you can get an exact overview of different types of angles.
i. The corresponding angles are always equal.
ii. An angle is formed only when two lines intersect.
iii. The alternate interior and alternate exterior angles are also equal. It is one of the most properties of types of angles.
iv. If we sum the pair of interior angles on the same side of the transversal, we will get a supplementary angle. It is an important one.
v. As we know that when two lines cross, they form vertically opposite angles. These angles are also equal.
Types of Angles Quiz
After reading the brief explanation about different types of angles, you can understand these angles. Now, you should give a quick quiz. This quick quiz will give an idea of whether you have understood the basic concepts of angles or not.
1. The measures of the two angles are 30° and 60°. These angles are;
a. Supplementary angles
b. Straight angles
c. Vertical angles
d. Complementary angles
2. The measures of the two angles are 130° and 50°. These angles are;
a. Supplementary angles
b. Straight angles
c. Vertical angles
d. Complementary angles
3. The angle whose exact measurement is 90° is known as;
a. Right angle
b. Reflex angle
c. Acute angle
d. Straight angle
4. The angle whose exact measurement is 180° is known as;
a. Reflex angle
b. Acute angle
c. Obtuse angle
d. Straight angle
5. The angle whose exact measurement is 0° is known as;
a. Straight angle
b. Acute angle
c. Zero angle
d. Reflex angle
6. An angle of 45° is a/an;
a. Acute angle
b. Obtuse angle
c. Straight angle
d. Reflex angle
7. An angle of 130° is a/an;
a. Acute angle
b. Zero angle
c. Reflex angle
d. Straight angle
You should choose the right answers to these questions. After choosing the right answers to these questions, you can post these answers in the comments box. We will check your answers and we will assign marks to you based on these questions. While assigning marks, we will also provide feedback about your concepts of types of angles.






1.Complementary angle
2.Supplementary angle
3.Right angle
4.Straight angle
5.Zero angle
6.Acute angle
7.Reflex angle